Linearyzacja dynamiczna

Jeśli dany jest układ dynamiczny opisany ogólnie nieliniowym równaniem różniczkowym postaci:

to możemy dokonać jego linearyzacji poprzez rozwinięcie w szereg Taylor'a wokół statycznego punktu pracy:

 

oraz odrzucenie części nieliniowej tego rozwinięcia czyli reszty oraz pochodnych rzędu wyższego niż pierwszy.

Warto w tym miejscu zaznaczyć, że wartość funkcji opisującej omawiany układ ma w tym punkcji wartość zero. Informację tę można niekiedy wykorzystać przy wyznaczaniu współrzędnych tego punktu.

Funkcja po rozwinięciu w szereg Taylor'a i odrzuceniu części nieliniowej ma postać:

 

Wartości wszystkich pochodnych liczone są w statycznym punkcie pracy.

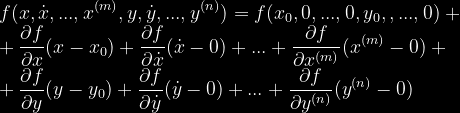
Przejdźmy do przykładu.
Mamy układ dynamiczny opisany następującym nieliniowym równaniem różniczkowym:

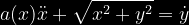W tym przypadku mamy nieliniowość dwóch typów. Po pierwsze wartość współczynnika a zależy od zmiennej x, a po drugie w równaniu występuje pierwiastek kwadratowy.
Przedstawmy to równanie w postaci funkcji czterech argumentów:

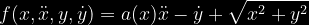Policzymy teraz pochodne występujące we wzorze na rozwinięcie w szereg Taylor'a podanym wyżej wokół statycznego punktu pracy

 

 

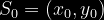
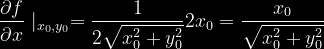
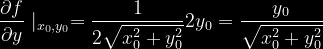
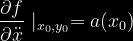
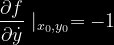
Po podstawieniu do wzoru otrzymujemy:

Co można również zapisać w następujący sposób:

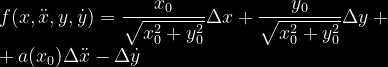
gdzie delty oznaczają małe odchylenia poszczególnych zmiennych od statycznego punktu pracy.

W razie jakichś niejasności, wątpliwości lub uwag proszę pisać w komentarzach.