Z układem statycznym mamy do czynienia wtedy, gdy wielkości wejściowe i wyjściowe tego układu są ze sobą związane równaniem algebraicznym, a nie różniczkowym (tak jak jest to dla układów dynamicznych). Ogólnie układ taki możemy opisać równaniem:
Wiedząc, że f(x,y)=0 oraz f(x0,y0)=0 otrzymujemy:
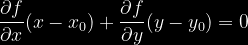 *Wartości pochodnych w powyższych wzorach wyznaczamy dla punktu pracy czyli podstawiamy za x, y odpowiednio x0, y0
*Wartości pochodnych w powyższych wzorach wyznaczamy dla punktu pracy czyli podstawiamy za x, y odpowiednio x0, y0
Ale wystarczy teorii, przejdźmy do praktyki.
Rozważmy nieliniowy układ statyczny opisany następującym równaniem algebraicznym:
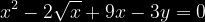 którego punkt pracy to (x0,y0)=(4,16).
którego punkt pracy to (x0,y0)=(4,16).
Wyznaczmy najpierw pochodne cząstkowe występujące w rozwinięciu:
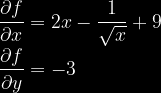
Liczymy ich wartości w punkcie pracy:
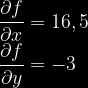
Podstawiamy obliczone wartości pochodnych oraz współrzędne punktu pracy do wzoru *:

Ale wystarczy teorii, przejdźmy do praktyki.
Rozważmy nieliniowy układ statyczny opisany następującym równaniem algebraicznym:
Wyznaczmy najpierw pochodne cząstkowe występujące w rozwinięciu:
Liczymy ich wartości w punkcie pracy:
Podstawiamy obliczone wartości pochodnych oraz współrzędne punktu pracy do wzoru *:
Otrzymaliśmy równanie liniowe, które w sposób przybliżony odzwierciedla nasz układ nieliniowy.
Poniżej przedstawiony został przebieg funkcji przed i po linearyzacji wraz z zaznaczonym punktem pracy.
W razie jakichś niejasności, wątpliwości proszę pisać w komentarzach do tego posta. Postaram się wyjaśnić w miarę możliwości.

Jeżeli szukacie sprawdzonego sklepu internetowego z elementami automatyki przemysłowej, to co powiecie na ofertę ze strony https://gigaom.pl/linkowe ? Są to specjaliści w swojej branży, którzy cieszą sie bardzo dobrą opinią.
OdpowiedzUsuń